【中2数学】内角と外角・角と平行線

2024/10/28

角と平行線の性質について覚えよう！

内角と外角

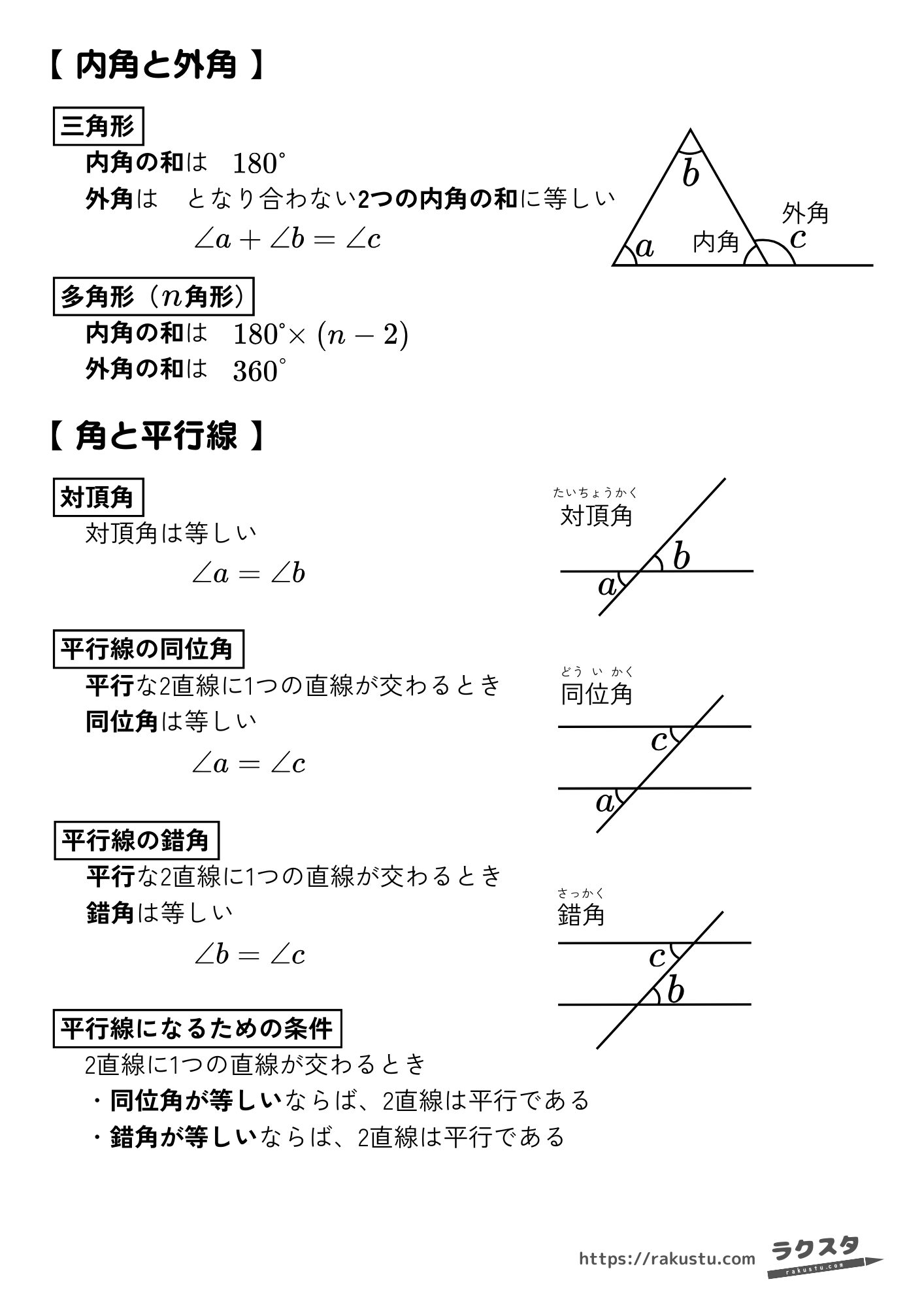
多角形の各頂点にできる角で多角形内にある角を内角、多角形の1辺とそのとなりの辺の延長とがつくる角を外角といいます。

三角形の内角の和は180°で、外角はとなり合わない2つの内角の和に等しいです。

三角形の内角の和は、180°
三角形の外角は、となり合わない2つの内角の和に等しい

多角形（n角形）の内角の和は、180°×(n−2) で求めることができます。

多角形の1つの頂点からその他の頂点へ対角線を引くと、(n−2)個の三角形ができます。

つまり、5角形であれば 5−2=3個の三角形、6角形であれば 6−2=4個の三角形ができます。

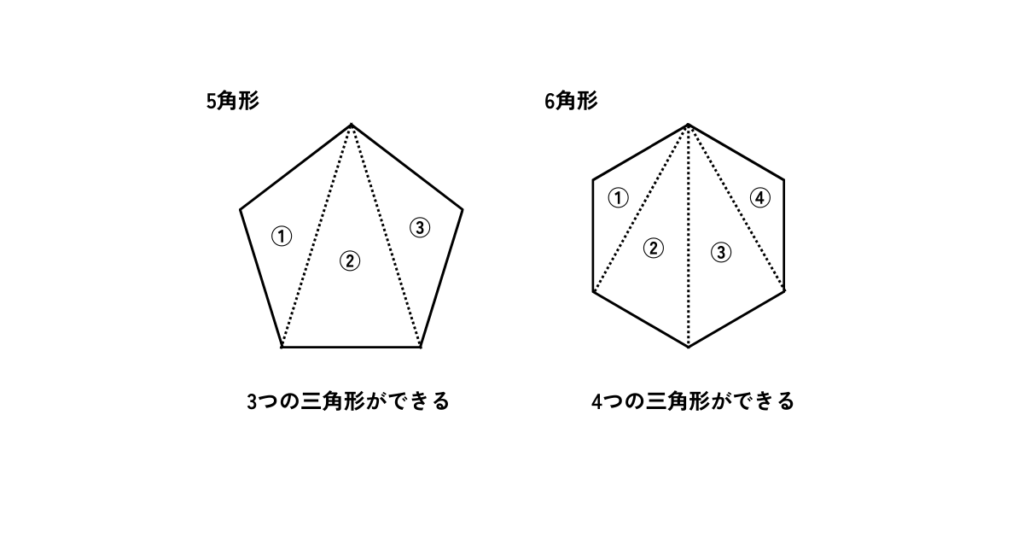
このことと、三角形の内角の和が180°であることを利用して、n角形の内角の和は 180°×(n−2) で求めることができます。

また、多角形の外角の和はすべて360°となります。

n角形の内角の和は、180° ×（n−2）
n角形の外角の和は、360°

平行な2直線、つまり平行線に1つの直線が交わるとき、同位角と錯角は等しくなるという性質があります。

同位角と錯角の位置関係は下のまとめプリントでチェック！

そのため、2直線に1つの直線が交わるとき

同位角が等しいならば、2直線は平行である
錯角が等しいならば、2直線は平行である

ということがいえます。

これらが、平行線になるための条件です。

苦手なところだけ効率よく学べる！

楽天ブックス

楽天ブックス